excel方差公式函数怎么用（用excel怎么进行方差和显著性分析）

前面我们说了方差分析中的单因素方差分析，但是在实际工作中，影响因素往往不止一个，需要考虑两个或以上因素对实验结果的影响。比如某公司销售汽车，在销售时，除了要关注汽车的外形、价格、耗油量等因素以外，还要考虑地区差异是否对销量有影响。今天来看一下双因素方差分析。

PART

01

双因素方差分析

如果将汽车颜色看成是影响销量的A因素，不同地区看成是影响销量的B因素，同时对A因素和B因素进行分析，即为双因素方差分析。

双因素方差分析是指分析两个因素，即行因素和列因素，对试验结果的影响的分析方法。当两个因素对试验结果的影响是相互独立的，且可以分别判断出行因素和列因素对试验数据的影响时，可使用双因素方差分析中的无重复双因素分析，即无交互作用的双因素方差分析方法。当这两个因素不仅会对试验数据单独产生影响，还会因二者搭配而对结果产生新的影响时，便可使用可重复双因素分析，即有交互作用的双因素方差分析方法。今天分享个可重复双因素分析的实例。

PART

02

双因素方差分析实例

实例应用：可重复双因素分析方法分析何种因素对效益有显著性影响

1、案例描述

某企业为了了解4种方案（因素2）在4个不同地区（因素1）的销售额状况，分别将4种方案投入4个地区进行试验，现有各个方案在不同地区的3天销售额数据，如下图所示，要求分析不同地区、不同方案，以及二者相交互分别对销售额的影响。

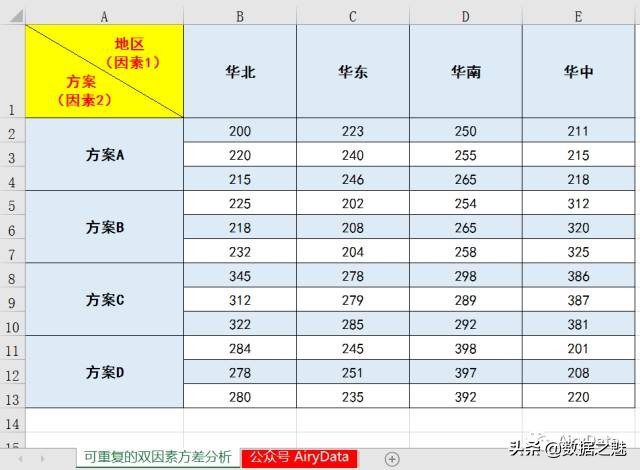
2、实例分析

在假设为5%的显著性水平下使用可重复双因素分析法推断不同地区、方案以及两者之间的交互作用中哪些因素对销售额有显著影响。

3、操作分析

第1步：选择分析工具并设置相关参数。打开“数据分析”——“方差分析：可重复双因素分析”，确定，在弹出的对话框中设置，“输入区域”为“$A$1：$E$13”，设置“每一样本的行数”为“3”，设置“α”为“0.05”，在“输出选项”选择“输出区域”，设置为“$G$2”，确定。需要注意的是“每一样本的行数”为各因素每一水平搭配使用的次数。

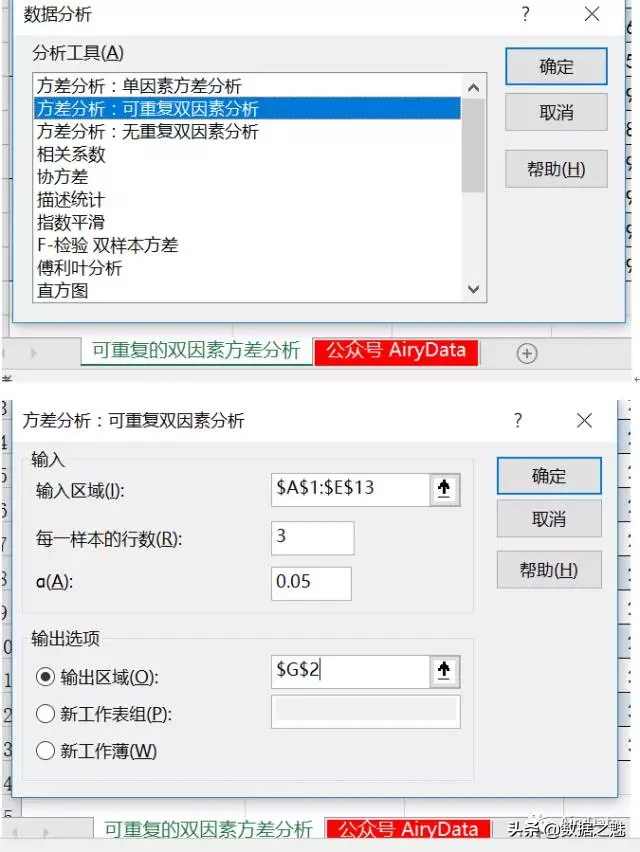
第2步：显示可重复双因素分析结果。如下图所示。

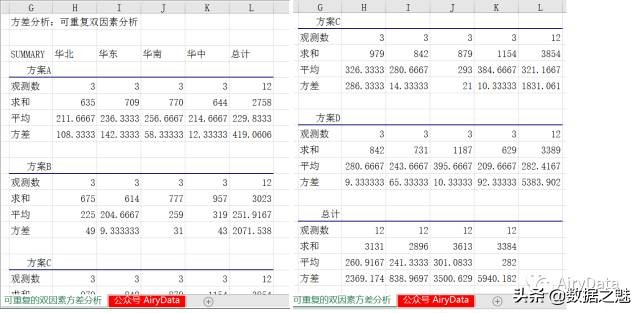
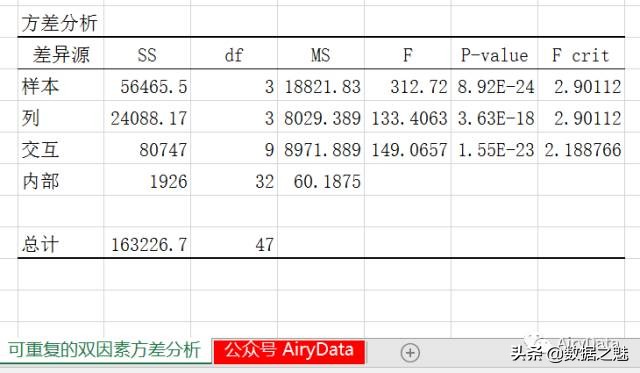
4、决策分析

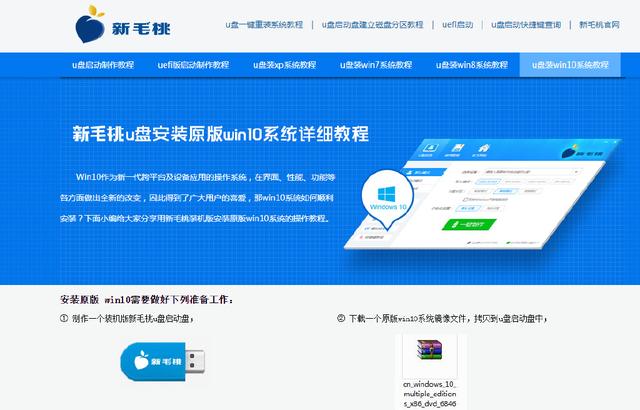
在分析结果第一部分的SUMMARY中，可看到各个方案对应地区的样本观测数、求和、样本平均数、样本方差等数据。在第二部分的“方差分析”中可看到，分析结果不但有样本[行因素/方案（因素2）]和列因素[地区（因素1）]的F统计量和F临界值，也有交互作用的F统计量和F临界值。

对比3项F统计量和各自的F临界值，样本、列、交互的F统计量都大于F临界值，说明方案、地区都对销售额有显著的影响。此外，结果中3个P-value值都小于0.01，也说明了方案和地区以及二者之间的交互作用对销售额都有显著影响，所以，该公司在制定后续的销售决策时，应考虑这些因素对销售额增长的作用。