今天的想法是用Canny边缘检测算法,建立一种可以勾画出图像上任何物体的边缘的算法。
首先,我们来描述一下Canny边缘检测器:
Canny边缘检测算子是一种边缘检测算子,它采用多级算法检测图像中广泛的边缘。它是由John F. Canny在1986年开发的。Canny还提出了边缘检测的计算理论,解释了该技术的工作原理。
Canny边缘检测算法由5个步骤组成:
- 降噪;
- 梯度计算;
- 非最大抑制;
- 双阈值;
- 滞后边缘跟踪。
应用这些步骤后,您将能够获得以下结果:

左侧的原始图像 - 右侧的已处理图像
最后值得一提的是,该算法是基于灰度图像的。因此,在进行上述步骤之前,首先要将图像转换为灰度。
降噪
由于场景背后涉及的数学主要基于导数(参见步骤2:梯度计算),边缘检测结果对图像噪声高度敏感。
消除图像噪声的一种方法是使用高斯模糊平滑图像。为此,图像卷积技术应用高斯核(3x3, 5x5, 7x7等)。核大小取决于预期的模糊效果。基本上,核越小,模糊就越不明显。在我们的例子中,我们将使用一个5×5的高斯核函数。
大小为(2k 1)×(2k 1)的高斯滤波核的方程为:
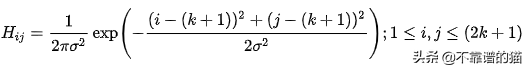
高斯滤波器核方程
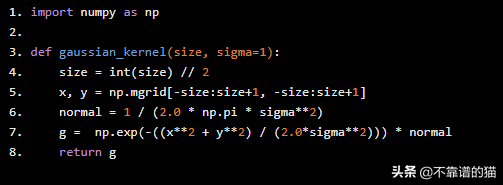
用于生成Gaussian 5x5内核的Python代码:
import numpy as np def gaussian_kernel(size, sigma=1): size = int(size) // 2 x, y = np.mgrid[-size:size 1, -size:size 1] normal = 1 / (2.0 * np.pi * sigma**2) g = np.exp(-((x**2 y**2) / (2.0*sigma**2))) * normal return g
应用高斯模糊后,我们得到以下结果:

梯度计算
梯度计算步骤通过使用边缘检测算子计算图像的梯度来检测边缘强度和方向。
边缘对应于像素强度的变化。要检测它,最简单的方法是应用filters,在两个方向上突出这种强度变化:水平(x)和垂直(y)
当平滑图像时,计算导数Ix和Iy。它可以通过分别用Sobel kernels Kx和Ky分别卷积I来实现:
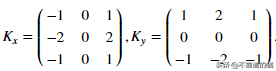
Sobel filters用于两个方向(水平和垂直)
然后,梯度的幅度G和斜率θ计算如下:
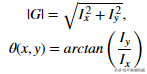
梯度强度和边缘方向
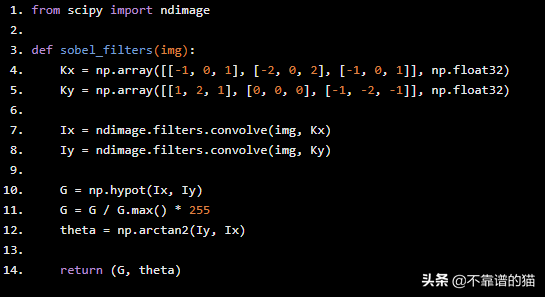
下面是Sobel滤镜应用于图像的方法,以及如何获得强度和边缘方向矩阵,Python代码如下:
from scipy import ndimage def sobel_filters(img): Kx = np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]], np.float32) Ky = np.array([[1, 2, 1], [0, 0, 0], [-1, -2, -1]], np.float32) Ix = ndimage.filters.convolve(img, Kx) Iy = ndimage.filters.convolve(img, Ky) G = np.hypot(Ix, Iy) G = G / G.max() * 255 theta = np.arctan2(Iy, Ix) return (G, theta)

模糊图像(左) - 梯度强度(右)
结果几乎是预期的,我们可以看到,一些边缘是厚的,另一些是薄的。非最大抑制步骤将有助于我们减轻厚的。
此外,梯度强度水平在0到255之间,这是不均匀的。最终结果的边缘应具有相同的强度(即白色像素= 255)。
非最大抑制
理想情况下,最终的图像应该有细边。因此,我们必须执行非最大抑制以使边缘变细。
原理很简单:算法遍历梯度强度矩阵上的所有点,并找到边缘方向上具有最大值的像素。
让我们举一个简单的例子:
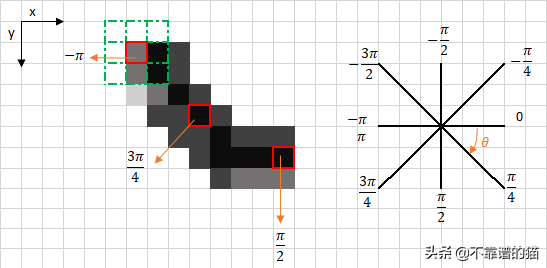
上图左上角的红色框表示被处理的梯度强度矩阵的一个强度像素。对应的边缘方向由橙色箭头表示,其角度为-pi弧度( /- 180度)。
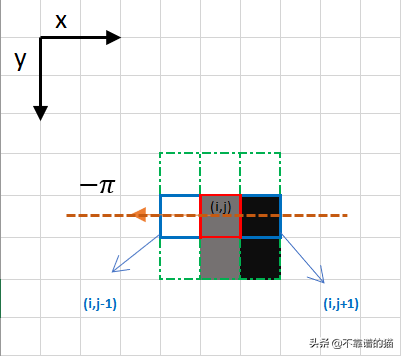
聚焦左上角的红色方块像素
边缘方向是橙色虚线(从左到右水平)。该算法的目的是检查在相同方向上的像素是否比被处理的像素强度高或低。在上面的例子中,正在处理像素(i,j),相同方向上的像素用蓝色(i, j-1)和(i, j 1)高亮显示。如果这两个像素中的一个比正在处理的那个更强,那么只保留更强的那个。像素(i, j-1)似乎更强,因为它是白色的(值255)。因此,当前像素(i, j)的强度值设置为0。如果边缘方向上没有具有更强值的像素,则保留当前像素的值。
现在让我们关注另一个例子:
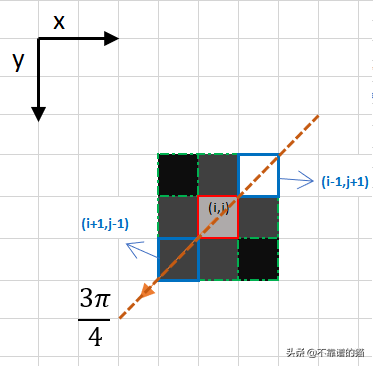
在这种情况下,方向是橙色虚线对角线。因此,该方向上最强的像素是像素(i-1,j 1)。
让我们总结一下。每个像素有2个主要标准(弧度的边缘方向和像素强度(0-255之间))。基于这些输入,非最大抑制步骤是:
- 创建一个初始化为0的矩阵,该矩阵与原始梯度强度矩阵的大小相同;
- 根据角度矩阵的角度值识别边缘方向;
- 检查相同方向的像素是否具有比当前处理的像素更高的强度;
- 返回使用非最大抑制算法处理的图像。
Python代码如下:
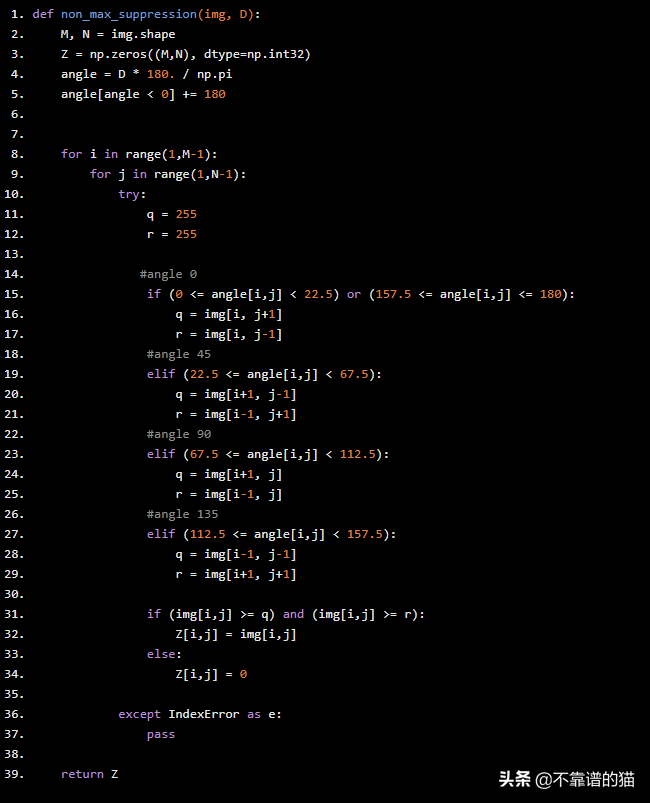
def non_max_suppression(img, D): M, N = img.shape Z = np.zeros((M,N), dtype=np.int32) angle = D * 180. / np.pi angle[angle < 0] = 180 for i in range(1,M-1): for j in range(1,N-1): try: q = 255 r = 255 #angle 0 if (0 <= angle[i,j] < 22.5) or (157.5 <= angle[i,j] <= 180): q = img[i, j 1] r = img[i, j-1] #angle 45 elif (22.5 <= angle[i,j] < 67.5): q = img[i 1, j-1] r = img[i-1, j 1] #angle 90 elif (67.5 <= angle[i,j] < 112.5): q = img[i 1, j] r = img[i-1, j] #angle 135 elif (112.5 <= angle[i,j] < 157.5): q = img[i-1, j-1] r = img[i 1, j 1] if (img[i,j] >= q) and (img[i,j] >= r): Z[i,j] = img[i,j] else: Z[i,j] = 0 except IndexError as e: pass return Z
结果是相同的图像,但边缘更薄。然而,我们仍然可以注意到边缘亮度的一些变化:一些像素似乎比其他像素更亮,我们将尝试在最后两个步骤中弥补这一缺陷。

非最大抑制的结果
双阈值
双阈值步骤旨在识别3种像素:强,弱和不相关:
- 强像素是指像素的强度如此之高,以至于我们确信它们有助于最终的边缘。
- 弱像素是具有不足以被视为强的强度值的像素,但是还不足以被认为与边缘检测不相关。
- 其他像素被认为与边缘无关。
现在你可以看到这两个阈值代表什么:
- 高阈值用于识别强像素(强度高于高阈值)
- 低阈值用于识别不相关的像素(强度低于低阈值)
- 具有两个阈值之间的强度的所有像素被标记为弱,滞后机制(下一步骤)将帮助我们识别可被视为强的那些和被认为是不相关的那些。
def threshold(img, lowThresholdRatio=0.05, highThresholdRatio=0.09): highThreshold = img.max() * highThresholdRatio; lowThreshold = highThreshold * lowThresholdRatio; M, N = img.shape res = np.zeros((M,N), dtype=np.int32) weak = np.int32(25) strong = np.int32(255) strong_i, strong_j = np.where(img >= highThreshold) zeros_i, zeros_j = np.where(img < lowThreshold) weak_i, weak_j = np.where((img <= highThreshold) & (img >= lowThreshold)) res[strong_i, strong_j] = strong res[weak_i, weak_j] = weak return (res, weak, strong)
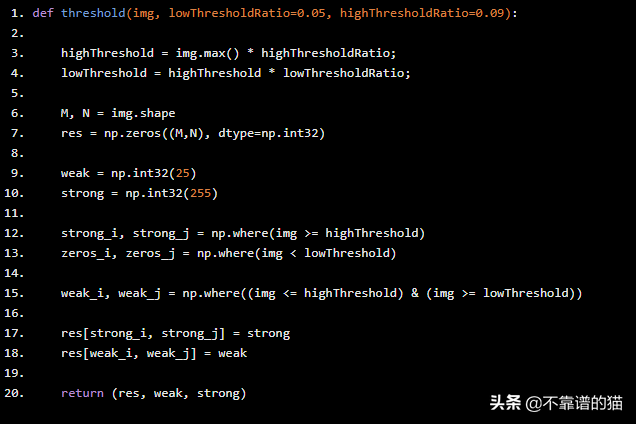
此步骤的结果是只有2个像素强度值(强弱)的图像:

非最大抑制图像(左) - 阈值结果(右)
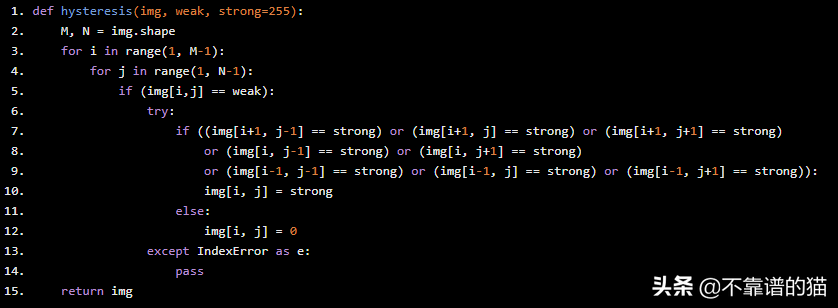
滞后边缘跟踪
根据阈值结果,当且仅当被处理像素周围至少有一个像素为强像素时,滞后由弱像素转换为强像素构成,如下所述:
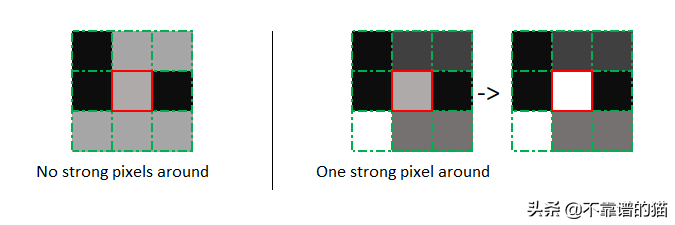
def hysteresis(img, weak, strong=255): M, N = img.shape for i in range(1, M-1): for j in range(1, N-1): if (img[i,j] == weak): try: if ((img[i 1, j-1] == strong) or (img[i 1, j] == strong) or (img[i 1, j 1] == strong) or (img[i, j-1] == strong) or (img[i, j 1] == strong) or (img[i-1, j-1] == strong) or (img[i-1, j] == strong) or (img[i-1, j 1] == strong)): img[i, j] = strong else: img[i, j] = 0 except IndexError as e: pass return img